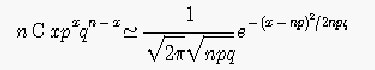|
||||
|
|
|||
1. 라플라스는 가난한 부모 밑에서 태어났다. 그는 수학적 능력이 뛰어나서 일찍이 좋은 교사직을 얻었고, 정치적인 기회주의자로서 프랑스 혁명의 불확실한 기간 동안 정권을 잡는 어떤 정당에라도 비위를 맞추었다. 그의 가장 뛰어난 업정은 천체역학, 활률론, 미분방정식, 측지학 분야에서 이루어졌다. 그는 기념비적인 두 작품, <천체 역학론, Traite de mecenique Celeste>(5권 1799-1825)과 <확률의 해석적 이론, Theorie analytique des probailites> (1812)을 발표하였는데, 각각 해박한 비전문가적인 해설이 붙어 있다. 그에게 '프랑스의 뉴턴'이란 별칭을 붙여준 다섯 권으로 된 <천체 역학론>은 라플라스 자신의 업저과 함께 그 이전의 모든 발견을 포함했고, 이로 인해 라플라스는 이 분야에서는 필적할 만한 사람이 없는 거장이 되었다. 이 논문과 관련해서 종종 말해지는 몇몇 일화를 다시 말하는 것도 흥미로울 것이다. 나폴레옹이 그의 논문에 신이 언급되지 않았다는 까다로운 지적을 했을 때 라플라스는 "폐하, 저는 그 가설이 필요치 않았습니다."라고 대답했다. 그리고 미국의 천문학자 나다니엘 보우디취는 라플라스의 논문을 영역할 때 "나는 라플라스 가 '따라서 그것은 명백하다'고 한 부분을 여러 시간 힘들여 부족한 부분을 공부하여 왜 그것이 명백한 가를 알아내지 않고서는 결코 이해하지 못한다.'고 언급했다. 라플라스의 이름은 우주 발생의 성운설, 퍼텐셜 이론의 소위 '라플라스 방정식(이 어느 것도 라플라스가 만든 것은 아니지만), 소위 '라플라스 변환' 그리고 행렬식의 '라플라스 전개'와 연관되어 있다. 라플라스는 뉴턴이 죽은 지 꼭 100년 후인 1827년에 죽었다. 어떤 보고에 의하면 그의 마지막 말은 "우리가 아는 것은 미미하고 모르는 것은 무한하다."였다. Pierre Simon Laplace(1749-1827)는 확률의 추론에 대한 4권의 저서를 남겼다. 이중에서 18세기 수학적 확률론의 역사에서 가장 의미있는 연구로 1773년 "Memoir on the probability of the Causes of Event", 1780년 "Memoir on Probabilities"을 손꼽는다. 2. 심프슨(1775)이후 독립적으로 진행된 오차의 확률분포에 대한 그의 관심은 우연하게도 O를 관찰, P를 관찰된 대상, E를 오차라 하면 O = P + E 의 관계를 맺게 되어 만약에 오차의 분포가 확률적으로 대칭이면 O와 P의 분포도 구할 수 있다는 생각을 정리 했다. 3. 이 생각은 결과에 대한 원인을
추정할수 있는 "Inverse Inference"를 낳게 했고 급기야 1774년에는 원인의
확률이 사전에 균등하게 주어졌을 때 베이즈 정리의 특수한 경우를 제공
했다. 즉, C1, ..., Cn을 원인이라 하고 E를 관심을 갖는 사건이라 하면 P(Ci|E) = P(E|Ci)/∑P(E|Cj) 를 나타낸다. 이는 오늘날 베이즈정리에서 P(Ci)=1/n, (모든 i에 대해서)를 적용한 것과 같다. 4. 1772년에서 1774년에 걸쳐 그는 시간의 축에서 세 시점에서 관측된 사건의 실제 일어난 시간 t를 찾는 문제에 몰두하였다. 그는 관측치가 t 로부터 x 만큼 차이가 날 확률 = f(x) 를 오차곡선이라 하고 이 함수를 어떻게 찾을 것인가에 관심을 기울였다. 특히 이 곡선의 성질은
실제 그의 문제는 1774년 f(x)=m/2 exp(-m|x|)인 Laplace distribution으로 결실을 맺었고 오늘날 이중지수분포(Double Exponential Distribution)이라 불려진다. 5. 라플라스는 1774-1786년의 일련의 논문에서 2항분포나 기하분포의 정규근사를 탐구하고 있었다. 이 논문들의 대부분은 [확률의 해석이론](1812)에 수록되어있다. [확률의 해석이론]제2권 3장에 De Moivre 와 같은 결과가 수록되어 있고, 제4장에서는 오차분포로서 정규분포를 유도하고 있다. 정리자체는 이미 1810년의 "대수의 함수로 임의의 공식의 근사 및 그것들의 확률에의 응용에 관한 암기책"에 나타나 있다. 이것이 최초의 중심극한정리의 발견과 증명이다. Laplace의 확률론에서의 중요업적중 중심극한정리는 통계학에서 백미로 곱을 수 있다. 1810년 4월 9일 아카데미에서 발표하였는데 De Moivre의 극한정리의 일반화로 어떤 합이나 평균은 n 이 크다면 정규분포로 근사한다. 는 사실이었다. 6. 2항분포의 극한분포로서 발견된 De Moivre와 라플라스의 결과는 현재 De Moivre-Laplace의 정리로서 알려져 있다. n이 충분히 클 때,
다음으로강의 12) Gauss-Laplace의 만
다음으로 라플라스와 가우스와의 만남에서 이루어진 많은 업적에 대해서 알아보자.
1. 가우스가 타고난 천재라면, 라플라스는 비교적 개인적인 성공에 대한 욕심이 많은 사람이었다. 라플라스에 관한 일화에서 그의 성격을 대강 짐작할 수있다. 라플라스라 젊어서 수학 교수직을 얻기 위하여 파리에 도착했을 때 저명한 사람이 쓴 추천서를 달랑베르에게 제출했으나 받아들여지지 않았다. 숙소로 돌아온 라플라스는 역학의 일반원리에 관한 재기 있는 편지를 달랑베르에게 썼다. 이것이 취직의 문을 열어주었고 달랑베르는 "귀하는 내가 당신의 추천서를 거들떠 보지도 않을 것을 아셨군요. 당신은 자신을 더 잘 소개했기 때문에 다른 것은 필요치 않군요."라고 답장하였다. 며칠 후 라플라스는 파리의 육군 사관학교의 수학 교수에 임명되었다. 가우스와 라플라스는 서로 자신의 생각들을 주고 받으면서 통계학에서 더욱 승화된 이론을 만들게 되는데 이러한 만남에서도 가우스와 라플라스간의 차이를 엿볼수 있다. 가우스가 라플라스가 생각해낸 분포를 토대로 완전한 정규분포의 모습을 찾아내는데 이 가우스의 논문을 보고 충격을 받게 된다. 가우스의 천재성에 약간의 충격과 부러움의 표시가 아니었나 하는 생각이 든다. 라플라스는 그전까지 자신이 만들어낸 분포가 당연히 자연의 모습인 정규분포라고 생각했기 때문이다. 하지만 라플라스도 가우스의 이론을 한층더 발전시켜 선형결합을 갖는 것중 가장 작은 분산을 갖는 "최소분산선형불편추정량(BLUE)"을 가진다는 가우스-마코프 정리를 제공하게 된다. 2. 1809 년 Carl Friedrich Gauss (1777 - 1855) 는
에서 행성의 궤도에 대한 연구를 마이어 등에 의해서 이미 행해진 연구와 같은 방향에서 접근하였다. 다만 그의 접근은 확률적 개념이 가미된 것이었다. 3. 행성궤도에 관한 미지의 방정식과 직접적인 관측치간의 차는 오차 E로 이들에 대한 확률값f(E)는 곡선을 이루며 f (E) = h/sqrt(3.14) exp(-h*h E*E), h>0 임을 찾아낸다. 여기서 h는 관측값의 정도에 대한 척도로 이 곡선을 Normal 혹은 Gaussian Curve 라 불렀다. 더군다나 이 곡선을 정립하는 과정에서는 일찍이 1774년에 Laplace가 오늘 날 베이즈 정리에 대한 그의 버전을 제시한 이론을 이용하였다. 4. 1810년 4월 Laplace는 Gauss의 이 논문을 보고 큰 충격을 받는다.
5. 12년후 Gauss는 Laplace의 이 이론을 한층 발전시켜 선형결합을 갖는 것중 가장 작은 분산을 갖는 "최소분산선형불편추정량 (Best Linear Unbiased Estimator : BLUE)"을 가진다는 Gauss-Markov 정리를 제공하게 된다. |
||||
질문) |
||||
|
||||